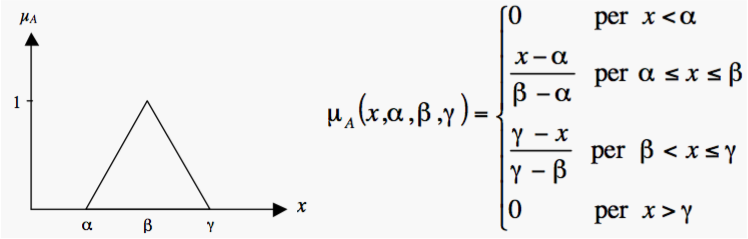Un sistema economico organizzato che vuole accrescere i propri standard di efficienza, deve sapersi orientare anche verso modelli innovativi di gestione e di controllo. Personalmente trovo molto interessante il modello che qui vado a descrivere, denominato “fuzzy logic”.
Introduzione alla logica fuzzy
La teoria della logica fuzzy è stata introdotta negli anni sessanta dall’ingegnere statunitense di origine iraniana Lotfi Zadeh. Essa si basa sulla definizione di insiemi “sfumati” con il fine ultimo di ottenere una rappresentazione più realistica di grandezze e concetti che sono per loro natura graduali, non dicotomici. Le variabili fuzzy non sono numeriche, ma linguistiche, ed assumono proprio valori come alto, basso, freddo, caldo. Si tenta di definire il grado di appartenenza, attraverso la cosiddetta funzione di appartenenza che nella logica bouleana può assumere solo due valori 0 o 1, mentre nella logica fuzzy, può assumere valori continui tra 0 e 1, in un processo che può essere definito inverso rispetto all’evoluzione digitale dell’era post-industriale. Le variabili fuzzy in coerenza con il modo di pensare umano e il suo modo di rappresentare i ragionamenti, sono caratterizzate dall’utilizzo di regole a volte approssimative, basate sul buon senso o sull’esperienza, ma difficilmente traslabili in termini analitici. Ecco perché la teoria fuzzy rifacendosi ai criteri decisionali umani, utilizza regole linguistiche e non matematiche nel definire il modo in cui le variabili si influenzano tra loro, non vi è l’utilizzo di formule o di complessi modelli analitici. Si può certamente affermare, che i sistemi fuzzy si comportano in modo soddisfacente proprio in quelle situazioni che una persona saprebbe gestire con facilità, ma che risultano le più difficili da affrontare con metodi analitici. Essi sono particolarmente adatti a lavorare in condizioni di incertezza e di disturbi nell’acquisizione dei dati. Si adattano bene a processi variabili nel tempo o fortemente non lineari, e quindi difficili da rappresentare con modelli matematici.
Impiego della logica Fuzzy
I sistemi gestiti con logica fuzzy sono in rapida espansione in molti campi, le aree di utilizzo sono prevalentemente due, i sistemi di controllo e i sistemi di supporto decisionale.
In molti sistemi fuzzy, le variabili d’ingresso sono espresse con valori numerici come ad esempio il valore espresso da un sensore o il costo a supporto di una determinata alternativa decisionale, spesso è richiesto un valore numerico anche per le risposte che il sistema deve fornire, per esempio l’entità di una spesa o il livello di rotazione di un magazzino. In tali situazioni, si presenta la necessità di relazionare il ragionamento fuzzy e i numeri, utilizzando operazioni di “fuzzificazione e defuzzificazione”, per traslare un valore associato ad un numero in un valore fuzzy e viceversa. In questa fase, si inserisce il processo d’inferenza fuzzy, utilizzato per interfacciare gli ingressi con le uscite corrette, ovvero associare a determinati valori delle variabili linguistiche d’ingresso (antecedenti) i corrispondenti valori delle variabili linguistiche d’uscita (conseguenti)
La caratteristica che differenzia i sistemi fuzzy di supporto decisionale rispetto ad altri modelli analitici utilizzati in supporto ai processi di trade off sta nel vantaggio concettuale. Ovvero si ha che mentre nei sistemi analitici, si cerca di trovare l’alternativa che massimizza una certa funzione obiettivo, rispettando una serie di vincoli, ergo la scelta della funzione obiettivo e la definizione dei vincoli risultano determinanti sull’esito del processo, nella logica fuzzy, obiettivi e vincoli sono gestiti allo stesso modo, entrambi sono espressi tramite le funzioni di appartenenza e il ruolo che assumono nel sistema viene ad essere stabilito da regole linguistiche così che è molto più agevole far convivere obiettivi concorrenti e fornire delle indicazioni al sistema senza dover necessariamente decidere se vanno usate come vincoli o come obiettivi. Questo, è da considerarsi un vantaggio di non poco conto poiché si evita la caratteristica dicotomia proprio di altri modelli analitici, in cui la funzione obiettivo permette di ordinare le alternative secondo un grado di preferenza, mentre i vincoli limitano lo spazio delle alternative, soprattutto nei casi in cui si vogliano conseguire più obiettivi specie se contrastanti.
Teoria Classica vs Teoria Fuzzy
Si ha che, un fuzzy set (insieme fuzzy) S può essere definito come un insieme di coppie ordinate costituite dagli elementi di X e dal corrispondente valore della funzione di appartenenza: S = {(x,fS (x)) | x ∈ X }.
Se l’insieme X è continuo si può rappresentare il fuzzy set S con la notazione: S=∫ X fS (x) / x; viceversa, se X è discreto, si ha che: S = ∑i μS (xi) xi
I simboli ∫ e ∑ indicano un’unione, mentre il simbolo “/” rappresenta il legame tra un valore di appartenenza e l’elemento cui si riferisce.
Le Funzioni di Appartenenza
A seconda del tipo di applicazione si possono definire funzioni di appartenenza anche molto diverse. Considerando un insieme A e una funzione µ, le funzioni di appartenenza più usate sono:
Funzione di appartenenza triangolare: definita con 3 parametri:
gli estremi α e γ e il punto di massimo β.
Funzione di appartenenza trapezoidale: definita con quattro parametri: gli estremi α e δ e i valori inferiore e superiore dell’intervallo di massimo β e γ.
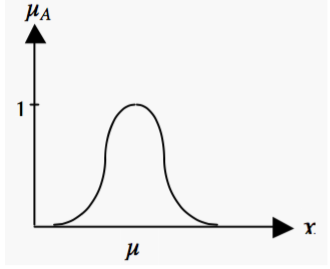
Funzione di appartenenza a campana: si può ottenere con gli stessi parametri della funzione triangolare, usando archi di parabola al posto di segmenti retti oppure con una gaussiana, fissando i parametri μ e σ della distribuzione.
La scelta delle funzione di appartenenza è determinante nella messa a punto di un sistema fuzzy, visto che essa determina le caratteristiche dei processi di fuzzificazione degli ingressi e defuzzificazione delle uscite. La fuzzificazione permette di calcolare il grado di appartenenza della variabile d’ingresso ad ogni fuzzy set, attraverso il valore numerico. La defuzzificazione calcola un valore reale per la variabile in uscita, a partire dal risultato fuzzy ottenuto nel processo di inferenza.
Regole Fuzzy
Le regole fuzzy rappresentano il punto di passaggio tra le conoscenze di tipo empirico descritte sopra e la loro elaborazione numerica. Tali regole sono qualitative e costituiscono la descrizione formale del sistema. Nel momento in cui esse vengono messe in relazione con le funzioni di appartenenza, definiscono un modello di sistema puramente numerico, su cui può lavorare anche un calcolatore. Una regola fuzzy è solitamente espressa con un costrutto del tipo if-then che può presentare uno o più antecedenti e uno o più conseguenti. Considerando per esempio una regola con un antecedente ed un conseguente, si ha la seguente forma: if x is A then y is B.
Struttura di un sistema fuzzy
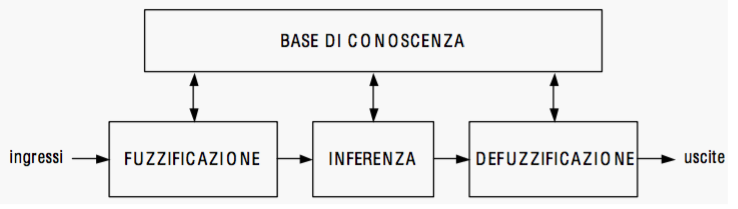
Un sistema fuzzy è costituito da quattro unità fondamentali, ossia la base di conoscenza e le 3 unità di calcolo: fuzzificazione, inferenza e defuzzificazione.
La base di conoscenza contiene tutte le informazioni sul sistema, che permettono alle altre unità di elaborare i dati d’ingresso per ottenere le uscite. Tali informazioni possono essere suddivise in data base e rule base. Il data base comprende la descrizione di tutte le variabili con le loro funzioni di appartenenza. Il rule base comprende le regole linguistiche d’inferenza.
Il motore d’inferenza è il cuore del sistema fuzzy. Esso determina lo stato delle uscite corrispondenti ad una determinata configurazione degli ingressi attraverso l’utilizzo delle informazioni contenute nella base di conoscenza.
La defuzzificazione può essere eseguita utilizzando varie strategie, nessuna delle quali si può considerare la migliore in assoluto. E’ compito del progettista stabilire quale è la metodologia che meglio si adatta alle esigenze poste dal problema contingente. Tra le strategie più usate si possono citare i metodo del massimo ed il metodo del baricentro. Il metodo del massimo prevede che il punto di defuzzificazione venga scelto lì dove la funzione di appartenenza dell’insieme d’uscita raggiunge il suo massimo. Se i punti di massimo sono molteplici, è possibile decidere se scegliere il primo (metodo del primo massimo, PM), l’ultimo (metodo dell’ultimo massimo, UM) o la loro media (metodo della media dei massimi, MM). Secondo il metodo del baricentro detto anche metodo del centroide o COG (Center Of Gravity), il valore calcolato per la defuzzificazione è quello relativo all’ascissa del baricentro della figura formata dalla funzione di appartenenza.
Un caso pratico: Le gestione del magazzino pezzi di ricambio di una compagnia aerea
L’introduzione di metodologie innovative nell’area della produzione (just in time, lean production ecc.) ha generato una visione dinamica del magazzino aziendale, attraverso l’introduzione di modelli organizzativi orientati ad una maggiore qualità nella gestione delle scorte, allo scopo di ridurre quei costi operativi diretti e indiretti che spesso rendono onerosa ed inefficiente la gestione globale degli approvvigionamenti. In questo conteso, l’inserimento di una filosofia di controllo innovativa come la logica fuzzy in un settore come quello aeronautico, ove spesso convivono criteri analitici piuttosto rigidi con soluzioni empiriche dovute al background del personale specializzato, può rappresentare davvero una rivoluzione gestionale in termini di costi, di qualità della performance e di sicurezza.
Prima di proseguire in questo business case, è necessario procedere nel catalogare i costi associati alle scorte, non senza tenere conto dei criteri imposti dalle normative aeronautiche Parte M (Annesso I al Regolamento europeo (CE) 2042/2003 del 20 novembre 2003:
- Costi delle immobilizzazioni di magazzino: Sono tutti quei costi che crescono con l’aumentare delle giacenze, ergo, possono essere considerati proporzionali alla quantità, al valore e al tempo di permanenza delle giacenze. Come indice di costo si utilizza il valore medio della giacenza nel periodo. Le principali voci che compongono i costi di immagazzinamento sono:
a) Costo opportunità del capitale immobilizzato nelle giacenze: ovvero la potenziale rendita finanziaria cui si rinuncia decidendo di mantenere un certo livello di scorte. Si calcola stimando quanto si sarebbe potuto ottenere investendo in altro modo il capitale impegnato nelle scorte. Come rendita minima si può considerare l’interesse di un deposito bancario, ma gli investimenti aziendali forniscono in genere rendite maggiori, e risulta quindi più realistica una stima basata sul valore del MARR.
b) Costi sostenuti per assicurarsi contro eventuali rischi d’incendio, furto o altro: sono anch’essi proporzionali al valore unitario del prodotto.
c) Costi operativi di immagazzinamento e movimentazione: possono essere di molti tipi e dipendono soprattutto dalle caratteristiche fisiche del prodotto, più nelle specifico so o riferiti ai: costi per lo spazio impiegato, ai costi per la logistica e le utility, costo del lavoro di movimentazione, ecc.
d) Costi dovuti ad obsolescenza delle parti di ricambio a vita limitata: sono probabilmente la voce di costo più volubile. Le regola aeronautiche, impongono una costante osservazione dei pezzi di ricambio in magazzino, soprattutto in relazione alle LLP (Life Limited Parts) che periodicamente devono essere ricertificati. Vi son poi alcune parti legate alla componentistica avionica, che perdono valore con il passare del tempo. In questi casi è determinante garantire un elevata rotazione delle scorte. - Costi delle ordinazioni: risultano in genere crescenti al diminuire delle giacenze. Per mantenere basso il livello delle scorte, servono infatti ordini frequenti di quantità ridotte.
- Costi per “rotture di magazzino”: Sono i costi o le perdite dovuti al mancato adempimento delle richieste di parti di ricambio della direzione tecnica con il conseguente stato di aeroplano “on ground”. I costi indiretti in questo caso sono: passeggeri da riproteggere, possibile impiego di aeromobile di backup con conseguente ferry flight e relativi costi, posizionamento della squadra di tecnici certificata per il delivery dell’aeroplano rimasto on ground per più di 24 ore, ecc. Si sommano così una notevole serie di costi che spesso diventano il vero tallone di Achille delle compagnie aeree, sino in molti casi a contribuire in maniera determinante al fallimento delle stesse. Tali costi risultano crescenti al diminuire delle scorte, poiché è più probabile soddisfare picchi di domanda se la scorta di sicurezza è elevata. Sono indubbiamente i costi più difficili da quantificare e da prevedere, per questa ragione non vengono inclusi nella maggior parte dei modelli analitici di gestione che prendono in considerazione solo le prime due categorie di costo.
Progettazione e Struttura del sistema Fuzzy
Si è progettato di suddividere la struttura generale del sistema di gestione delle parti di ricambio, in due sezioni interagenti, una algebrica di aggiornamento dell’inventario ed una fuzzy di calcolo dei fabbisogni. L’aggiornamento dell’inventario, è quindi eseguito in maniera deterministica, mentre alla logica fuzzy il compito di gestire il problema dell’incertezza legata ai fabbisogni. La prima sezione del progetto non presenta quindi caratteristiche distintive particolari. Con essa si attua in sostanza l’aggiornamento continuo dell’archivio delle giacenze, attraverso un processo di tipo sequenziale nel rispetto delle normative aeronautiche precedentemente citate.
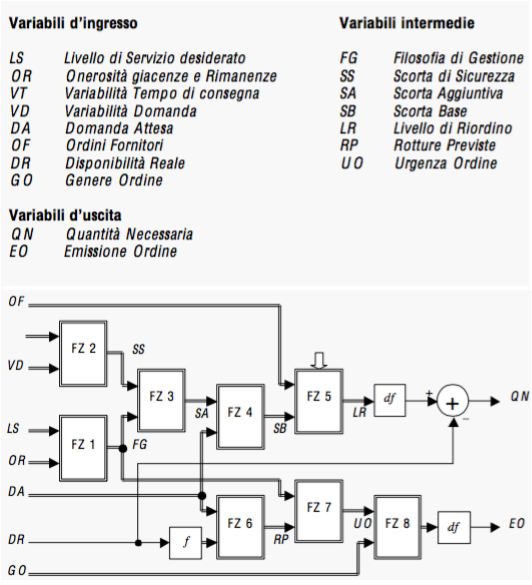
La sezione di calcolo dei fabbisogni è invece un vero e proprio sistema fuzzy, composto di più blocchi d’inferenza. La progettazione di tale sistema ha richiesto un’analisi accurata, di seguito, tralasciando le descrizione di tale analisi, sono illustrate le caratteristiche del sistema fuzzy così per come concepito, rispettando la sequenza logica delle fasi di progettazione. Sono state definite per il sistema otto variabili d’ingresso e due variabili d’uscita. Le variabili scelte si ritiene che possano garantire il giusto compromesso tra le due esigenze opposte di completezza e semplicità. È molto importante che non siano trascurate variabili significative per il problema da affrontare, ma è altrettanto importante che il sistema non risulti appesantito sia in progettazione che in esecuzione da variabili o blocchi di calcolo di peso marginale. Di seguito la grafica del progetto e la descrizione delle variabili di entrata, di uscita e intermedie:
Le variabili e i blocchi fuzzy sono rappresentate dalle linee doppie, le variabili semplici e gli operatori algebrici sono rappresentate dalle linee semplici. Le variabili d’ingresso devono sempre essere sottoposte all’operazione di fuzzificazione che è sottintesa per tutte le variabili tranne che per la variabile disponibilità reale (DR), essendo quest’ultima utilizzata sia come variabile fuzzy sia con il suo valore numerico effettivo. Si possono osservare i due percorsi di calcolo che portano alle due uscite: il primo percorso determina la quantità necessaria al ripristino delle scorte (QN), il secondo decide se è opportuna l’emissione dell’ordine (EO).
Determinazione della quantità necessaria (QN)
Questa parte del sistema coinvolge sette delle otto variabili d’ingresso. Il fabbisogno è deciso in base alla situazione effettiva delle giacenze, ai consumi previsti e a una serie di variabili tendenti a influenzare opportunamente la quantità di scorte ritenuta più adatta nelle diverse situazioni. Per una maggiore comprensione della sequenza logica delle operazioni, è opportuno descrivere il funzionamento andando a ritroso, partendo dall’uscita finale per giungere ai primi blocchi di calcolo e alle variabili d’ingresso:
la variabile d’uscita quantità necessaria (QN), che in questa parte del sistema rappresentano una variabile numerica non fuzzy, è calcolata algebricamente come differenza tra la variabile intermedia livello di riordino (LR) e le disponibilità reali (DR). L’uscita fuzzy della prima parte del sistema è la variabile LR, che rappresenta la quantità a cui si ritiene debbano essere ripristinate le giacenze. Su tale variabile si deve eseguire l’operazione di defuzzificazione, al fine di ottenere il valore numerico da cui sottrarre l’entità delle disponibilità reali.
Nel determinare il livello di riordino si deve tenere conto di eventuali ordini in corso. Trascurare l’eventuale esistenza di lotti di merci in arrivo porta infatti a sovrastimare i reali fabbisogni. Nel sistema la questione è affrontata nel blocco 5, che stabilisce il livello di ordini dai fornitori (OF) attualmente in corso e dal valore della scorta base (SB) definibile come la quantità di ripristino al netto degli ordini in corso e determinata dal blocco 4, tenendo conto del contributo della domanda attesa (DA) e della scorta aggiuntiva (SA).
La domanda attesa è una stima dei consumi che si avranno nel corso del “lead time”, la scorta aggiuntiva serve ad introdurre nella gestione le fonti d’incertezza e gli orientamenti strategici dell’azienda. Essa viene calcolata nel blocco 3, a partire dalla variabile filosofia di gestione (FG) e dal valore della scorta di sicurezza (SS), uscite dei primi due blocchi fuzzy.
Nel blocco 1 gli ingressi sono costituiti dalle due variabili: livello di servizio desiderato (LS) e onerosità di giacenze e rimanenze (OR). Queste ultime sono direttamente legate alla strategia aziendale, in quanto influenzano la filosofia di gestione, determinando sia la scorta aggiuntiva che l’urgenza di una ordinazione.
Nel blocco 2 viene definita la variabile scorta di sicurezza (SS), introdotta per assicurarsi un margine di errore nelle stime. Gli ingressi del blocco sono la variabilità della domanda (VD) e la variabilità dei tempi di consegna (VT) che influenzano in modo simile la gestione valutando il livello d’incertezza insito nel processo decisionale.
In conclusione si può certamente affermare che i modelli fuzzy soprattutto in certe aeree di intervento possono davvero rappresentare uno sbocco innovativo non di poco conto, credo che in alcuni modelli di business ad alta densità di variabili esogene quali appunto l’aviazione, uscire dalla dicotomia alternative/vincoli può rivelarsi un ottimo supporto nel perseguire un sempre maggiore livello di efficienza ed efficacia.